library(SwimmeR)
library(rvest)
library(purrr)
library(dplyr)
library(ggplot2)
library(stringr)
library(flextable)

flextable_style <- function(x) {
  x %>%
    flextable() %>%
    bold(part = "header") %>% # bolds header
    bg(bg = "#D3D3D3", part = "header") %>%  # puts gray background behind the header row
    autofit()
}

Web Scraping to Get Results

As we often do around here we’re going to scrape a bunch of swim meets from some online repository. The strategy here is roughly the same as in my previous post about webscraping with SwimmeR.

We’ll get out target link (sec_v_link), and css node (".xspLinkViewColumn") and then use html_nodes and html_attr to get a list of links. We’ll then cut that list down to what we want with by using map_lgl to apply str_detect across it.

sec_v_link <-
  "http://www.swimdata.info/NYState/MeetResultsRepository.nsf/Sec5Girls.xsp"

page_contents <- read_html(sec_v_link)

links <-
  html_attr(html_nodes(page_contents, ".xspLinkViewColumn"), "href")

sectional_links <- links %>%
    .[map_lgl(., str_detect, "http")] %>%
    .[map_lgl(., str_detect, "Meet")] %>%
    .[map_lgl(., str_detect, "Sec5")] %>%
    .[!map_lgl(., str_detect, "nyhsswim")] %>% 
    .[!map_lgl(., str_detect, "\\.zip")] %>%
    .[!map_lgl(., str_detect, "\\.nsf")]

The 2020 results aren’t included in our scraped results (they must not have been added to the repository yet). We can add them to our list manually.

links_2020 <-
  c(
    "http://www.section5swim.com/Results/GirlsHS/2020/Sec5/C/Single.htm",
    "http://www.section5swim.com/Results/GirlsHS/2020/Sec5/B/Single.htm",
    "http://www.section5swim.com/Results/GirlsHS/2020/Sec5/A/Single.htm"
  )

sectional_links <- c(sectional_links, links_2020)

Now we just need to map our SwimmeR functions over the list of links. First read_results to read in the raw files, and then swim_parse to parse them. We’ll do this inside of safely in case there are bad links (there aren’t, but still) and discard problematic imports with discard_errors.

Running this code will take a while. You can also download the results directly from my github.

results_raw <- map(sectional_links, read_results)
results <- map(results_raw, safely(swim_parse, otherwise = NA))

results <- SwimmeR:::discard_errors(results)

We can name each file based on its link, and stick them all together into one dataframe with bind_rows.

meet_names <- sectional_links %>% 
  str_extract("\\d{4}/Sec5/[:upper:]") %>%
  str_replace("/Sec5/", "_")

names(results) <- meet_names

results <- dplyr::bind_rows(results_2, .id = "Meet")

---

Cleaning Up the Data

We’d like to separate the Meet column into two pieces of information, which means two columns. The first is the Year in which the meet took place - pretty simple. The second is we’ll Class, which is the term used by Section V to denote the size of the schools competing at a given meet. Class A schools are the largest, with Class B being smaller, and Class C being the smallest. This means that we’re usually looking at three meets per year, over 21 years, for a total of 63 meets. The reality though is that there’s only 60 meets because in three separate years (2000, 2001 and 2016) Section V attempted to realign the classes and have only two meets, Class A and Class B. This meant that in those years the larger Class B schools went up to Class A and all of the Class C schools ended up in Class B.

results <- results %>% 
  filter(str_detect(Event, "Swim\\-off") == FALSE) %>% # remove swim offs
  mutate(Year = as.numeric(str_extract(Meet, "\\d{4}")), # get meet year
         Class = str_extract(Meet, "[:upper:]")) %>% # get meet class
  mutate(Finals_Sec = sec_format(Finals_Time)) %>% # convert finals time to seconds format for doing math
  mutate(Event = str_remove(Event, "Girls "), # shortening event names for easier plotting
         Event = str_remove(Event, "style")) # shortening event names for easier plotting

---

Top 8 Times

The variable I want to look at is the average time for all swimmers in the top 8 of a given event at a given meet for each year. Looking at individual times is just too noisy. Sometimes athletes have especially good (or bad) meets, different people taper for different meets, seniors graduate, it’s too much noise. The top 8 though is a reasonable metric for what’s going on in an event though.

I’m going to exclude diving from this analysis, not because it can’t apply, but because diving results are much much noisier than swimming results, which makes plotting a pain.

results_summary <- results %>% 
  group_by(Class, Event, Year) %>%
  filter(Place <= 8) %>% # get top 8 finishers
  summarise(Top_8_Avg = round(mean(Finals_Sec, na.rm = TRUE), 2)) # calcuate average time of top 8 swims

Just to see what we’ve got, let’s look at all four 100 yard races.

results_summary %>%
  filter(str_detect(Event, 'Div') == FALSE) %>% # don't want to include diving
  filter(str_detect(Event, "100") == TRUE) %>% # only want 100s
  ggplot(aes(x = Year, y = Top_8_Avg, color = Class)) +
  geom_point() +
  geom_line() +
  facet_wrap(. ~ Event) +
  theme_bw() +
  labs(y = "Average Top 8 Time (s)",
       title = "Average Top 8 Time Trend by Event - 100s")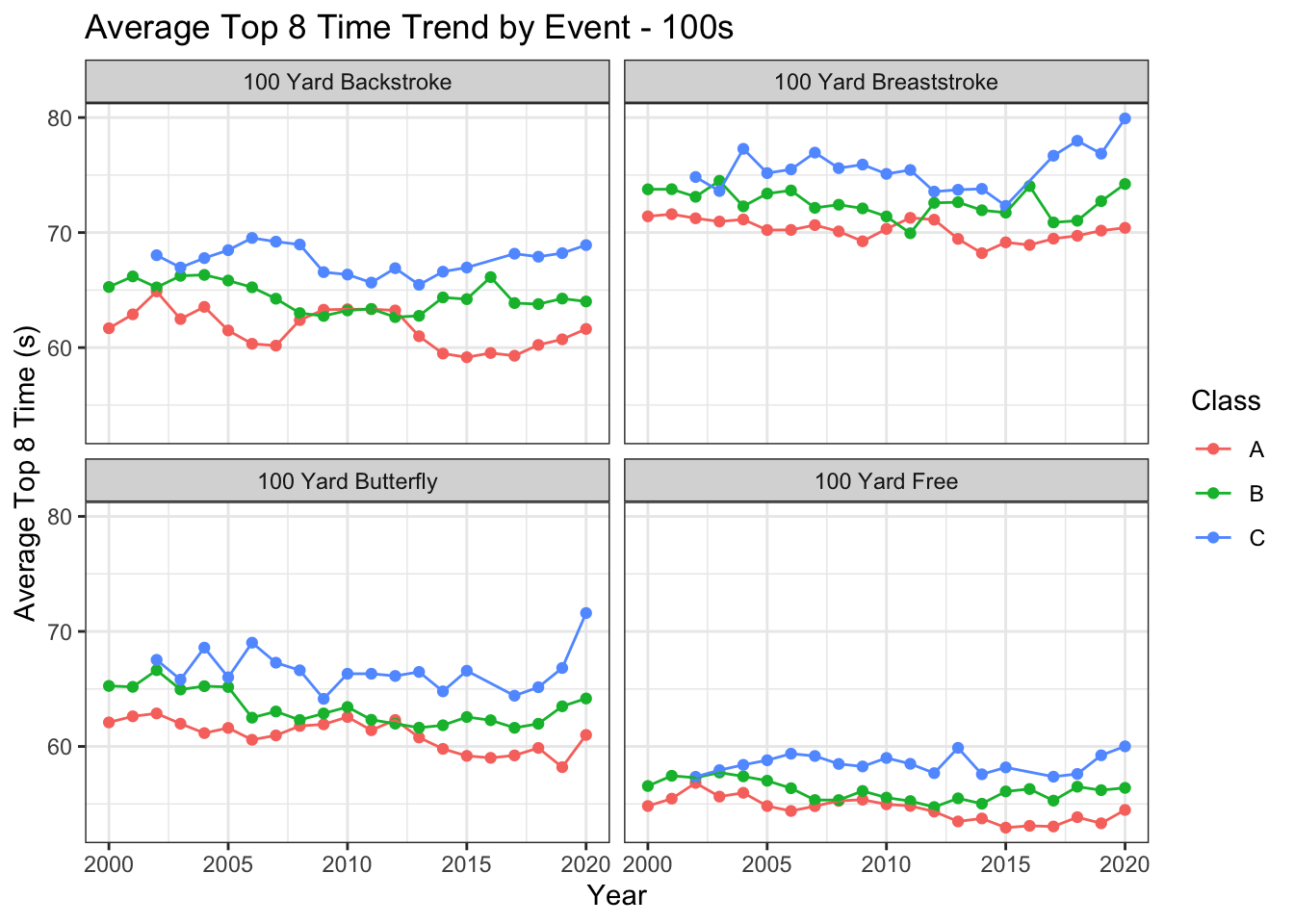

Times for these races look to maybe trend down, i.e. swimmers are getting faster and faster. The trend, if it even actually exists, certainly isn’t monotonic. It’s noisy and maybe imaginary. Let’s calculate the percent change year to year, for each event and class.

Percent change will also allow us to directly compare events of different lengths, where comparing absolute times won’t, because longer races just naturally take longer more time to complete.

results_summary <- results_summary %>%
  group_by(Event, Class) %>%
  arrange(Year, .by_group = TRUE) %>% # arrange by year within group
  mutate(Perc_Change = round((Top_8_Avg - lag(Top_8_Avg, default = NA)) / # calculate year-to-year percentage change
                               Top_8_Avg * 100, 2)) %>%
  mutate(Perc_Change = case_when(str_detect(Event, "Diving") ~ Perc_Change * -1, # in case someone wants to include diving
                                 TRUE ~ Perc_Change))

results_summary %>%
  filter(str_detect(Event, 'Div') == FALSE) %>% # don't want diving
  ggplot(aes(x = Year, y = Perc_Change, color = Class)) +
  geom_point() +
  geom_line() +
  facet_wrap(. ~ Event) +
  theme_bw() +
  theme(axis.text.x = element_text(angle = 70, hjust = 1)) +
  labs(y = "Year-To-Year Percentage Change (%)",
       title = "Percent Change in Average Top 8 Time Trend by Event")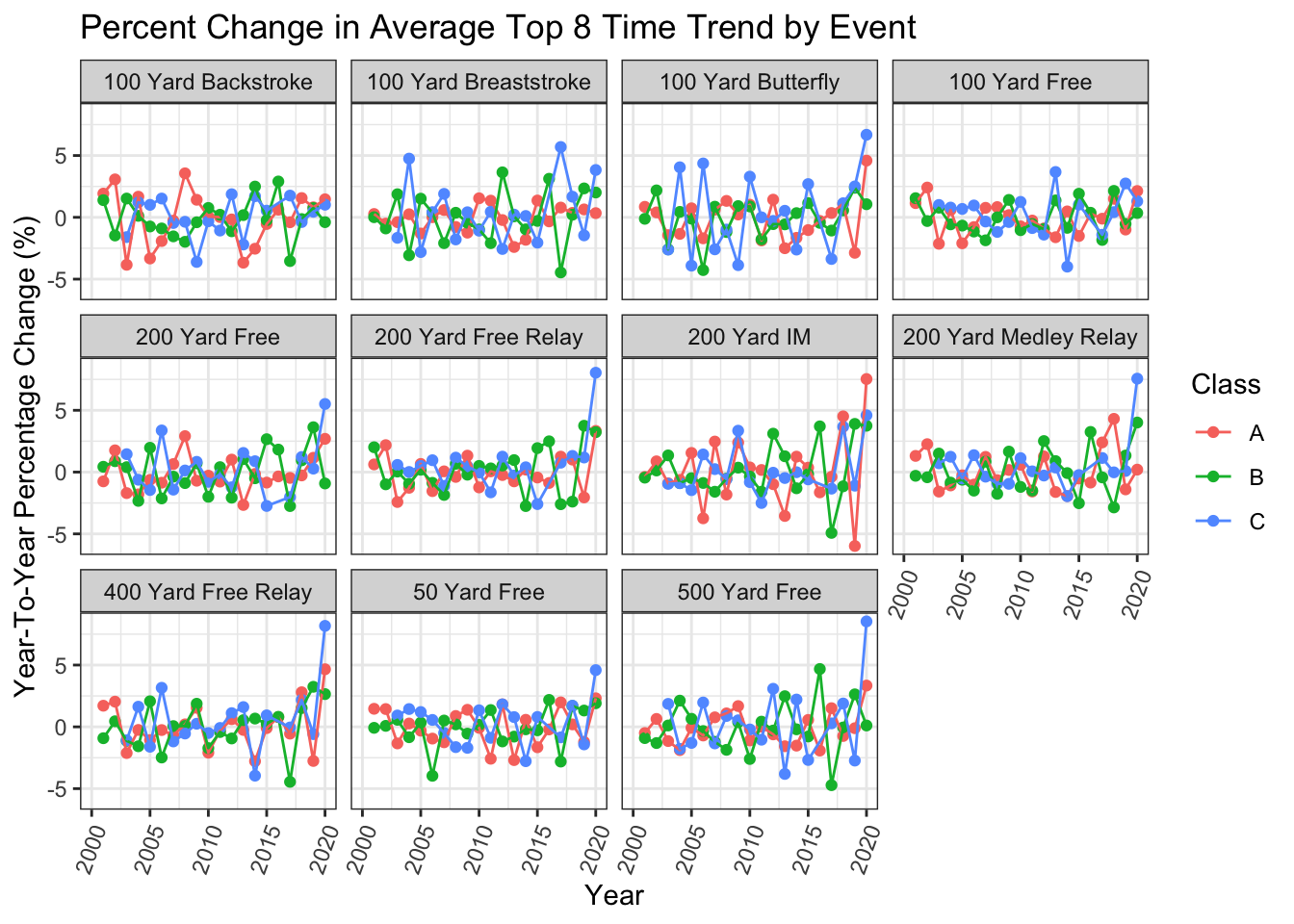

It’s not super clear, but it looks to me like there’s a percentage increase in times in 2020. Let’s look at some actual numbers and get some clarity.

results_summary <- results_summary %>%
  mutate(Direction = case_when(Perc_Change > 0 ~ 1, # get directions of changes (not magnitudes)
                               Perc_Change <= 0 ~ -1))

results_summary %>% 
  filter(str_detect(Event, "Diving") == FALSE) %>% # don't want diving
  filter(Year < 2020) %>% # don't want year 2020 results (setting baseline)
  ungroup() %>%
  summarise(Perc_Mean = round(mean(Perc_Change, na.rm = TRUE), 2)) %>% # average year-to-year change for entire data set
  flextable_style()

Average change per year is -0.08%, meaning that on average the top 8 swimmers get ever so slightly faster year to year. We were right that there was an overall negative trend to those plots. It is small though.

---

Directions

Let’s put aside magnitude for a moment and just consider the sign on Perc_Change. If the sign is negative that means the top 8 swimmers in a given event/meet/year combination were faster on average than the top 8 swimmers from that same event/meet the previous year. If the sign is positive then the reverse is true, the top 8 swimmers got slower on average compared to the previous year. It’s also possible that Perc_Change could be zero, although that doesn’t happen in this data set. We’ll treat the possibility though by including zero with the positives, because if you’re not improving then what are you doing?

results_odds <- results_summary %>%
  filter(str_detect(Event, "Diving") == FALSE) %>% # don't want diving
  filter(Year < 2020) %>%  # don't want year 2020 results
  group_by(Event, Class) %>% 
  summarise(Decline = sum(Perc_Change >= 0, na.rm = TRUE), # get number of declines (worse times year-to-year)
            Improvement = sum(Perc_Change < 0, na.rm = TRUE)) %>% # get number of improvements (better times year-to-year)
  mutate(Perc_Decline = Decline/(Improvement + Decline) * 100, # percentage of declines
         Perc_Improvement = Improvement/(Improvement + Decline) * 100) # percentage of improvements

What we’ve calculated here is the rates at which the top 8 swimmers in each event of each meet are faster (negative sign, Improvement) or slower (positive sign, Decline) than the top 8 swimmers from that same meet and event the previous year. We could compare the 2020 results to these probabilities, but that actually wouldn’t be very interesting. All the probabilities are about 50/50, and there’s only one 2020 result for each meet/event combination. Either outcome, improvement or decline, for the 2020 results overall would make sense given a 50/50 probability.

What we need to do instead is get an overall probability for a improvement or decline outcome, and then compare the 33 meet/event outcomes from 2020 to that probability. (This is admittedly a bit sneaky, and there might be other, better, ways to handle it. Leave comments with your own approaches if you feel so moved.)

results_odds_pre2020 <- results_odds %>% 
  ungroup() %>% 
  summarise(Perc_Decline = round(mean(Perc_Decline), 2), # overall percent decline
            Perc_Improvement = round(mean(Perc_Improvement), 2)) # overall percent improvement

results_odds_pre2020 %>% 
  flextable_style()

Here’s something interesting - although year-to-year change is an ever-so-slight improvement, the overall probability of a improved result (that is, a collective improvement of the top 8 swimmers in a meet) is actually less than that of a declining result. I suspect the reason for this is that improved results are driven by exceptional swimmers in the first few places, who effectively improve the top 8 average by a wide margin. Those swimmers only come along occasionally, but when they do their impacts are significantly. I’m not going to attempt to demonstrate this today, but it could be done with this data set. (Also, I might be wrong. Stranger things have happened.)

In any case what we have here, for years 2000-2019 is basically a coin flip. We expect that the top 8 swimmers in an average event in given meet will be faster than the year previous 47.8% of the time, and slower 52.2% of the time.

Let’s see what happened in 2020.

results_2020_odds <- results_summary %>%
  filter(str_detect(Event, "Diving") == FALSE) %>% # don't want diving
  filter(Year == 2020) %>% # want results from 2020
  ungroup() %>% 
  summarise(Decline = sum(Perc_Change >= 0, na.rm = TRUE), # how many declines in 2020
            Improvement = sum(Perc_Change < 0, na.rm = TRUE)) # how many improvements in 2020

results_2020_odds %>% 
  flextable_style()

That’s 31 declines and 2 improvements. This looks suspicious, given that we expect declines and improvements to occur at about the same rate. We can check our suspicion using prop.test, which we previously used during the State-Off to see if seniors really do rule.

We need to state a formal null hypothesis to use prop.test, which in this case is “the results from 2020 match those from previous years in that the likelihood of the top 8 swimmers from in a given meet/event from 2020 being collectively slower than the top 8 swimmers from from that same meet/event in 2019 is 0.522”. We also need a significance value, for which we’ll use the standard 0.05. If the p-value from prop.test is less than our significance value then we can reject the null hypothesis.

prop.test(x = results_2020_odds$Decline[1], n = sum(results_2020_odds$Decline, results_2020_odds$Improvement), p = results_odds_pre2020$Perc_Decline[1]/100) # print prop test results

## 
##  1-sample proportions test with continuity correction
## 
## data:  results_2020_odds$Decline[1] out of sum(results_2020_odds$Decline, results_2020_odds$Improvement), null probability results_odds_pre2020$Perc_Decline[1]/100
## X-squared = 26.336, df = 1, p-value = 2.868e-07
## alternative hypothesis: true p is not equal to 0.478
## 95 percent confidence interval:
##  0.7837902 0.9894327
## sample estimates:
##         p 
## 0.9393939

The p-value from out test is 2.868239410^{-7}, which is much less than 0.05, so we reject the null hypothesis. Something is different about the behavior of the average top 8 times in 2020 versus the previous years.

We should check the rest of the years too though.

results_pval_allyears <- results_summary %>%
  filter(str_detect(Event, "Diving") == FALSE) %>% # don't want diving
  filter(Year > 2000) %>% # year 2000 doesn't have a previous year, so no values
  group_by(Year) %>% 
  summarise(Decline = sum(Perc_Change >= 0, na.rm = TRUE), # total declines
            Improvement = sum(Perc_Change < 0, na.rm = TRUE), # total improvements
            Total = sum(Improvement, Decline), # total events
            P = 0.522) %>% # calculated above
  rowwise() %>% # need to do next calcuation across rows not dnow columns
  mutate(P_Val = round(prop.test(x = Decline, n = Total, p = P)$p.value, 3)) # get the p-value for every year

row_id_fail_to_reject <- # values where P_Val is greater or equal to than the significance value, should be green, fail to reject null hypothesis
  with(results_pval_allyears, round(P_Val, 2) >= 0.05)

row_id_reject <- # values where P_Val is less than the significance value, should be red, reject null hypothesis
  with(results_pval_allyears, round(P_Val, 2) < 0.05)

col_id <- c("P_Val") # which column to change background color in

results_pval_allyears %>%
  select(-P) %>% 
  flextable_style() %>%
  bg(i = row_id_fail_to_reject, # color rows with p-value >= 0.05 green
     j = col_id,
     bg = "green",
     part = "body") %>%
  bg(i = row_id_reject, # color rows with p-value < 0.05 red
     j = col_id,
     bg = "red",
     part = "body") %>%
  colformat_num(j = "P_Val",
                big.mark = ",",
                digits = 3) %>%
  autofit()

What we’re seeing is that while yes, 2020 was a weird year, with the biggest discrepancy between improvement and decline in the top 8 results in the data set, 2018 was also a weird year. I don’t know why that’s the case, but it is.

We can look at the total change in Perc_Change across all meet/events for a given year to get a magnitude for weirdness.

results_summary %>%
  filter(str_detect(Event, "Diving") == FALSE, # don't want diving
         Year %!in% c(2000, 2001, 2016)) %>% # these years are different, no Class C meet
  group_by(Year) %>% 
  summarise(Total_Perc_Change = sum(Perc_Change, na.rm =TRUE), # add up all Perc_Changes
            Avg_Perc_Change_Per_Event = round(Total_Perc_Change/33, 2)) %>% # 33 is number of events across the three class meets
  flextable_style()

While 2018 remains a strange year, the total percentage change in average top 8 time for 2020 is more than three times larger than that for 2018. 2020 is ~3x weirder than 2018, compared to the other years. 2020 also has, specifically, an increase in time, meaning a decline in performance. This is doubly bad. The NYS championships being canceled means this is the last meet for the high school season, so maybe more people would have tapered for it (I don’t know what the USA season holds, maybe there are worthy taper meets there).

---

Answering Our Questions

At the beginning of the post I asked these two questions:

1. Were the 2020 results different from other years?
2. If so, in what way, re: performances, where they different?

Regarding question #1 - yes, 2020 was different.

Regarding question #2 - The meet normally operates close to equilibrium, with the average top 8 time changing less than 1% year to year. Times go up and down around this equilibrium, going up just over 50% of the time, and down just under 50%. Downward movements though are of a slightly larger magnitude, meaning that overall the meets get slightly faster with time. Not in 2020 though. We saw that the roughly 50/50 split between times improving and backsliding did not hold for 2020. Similarly we saw that the average top 8 time increased (got worse) by over 3%, more than 3x the normal.

---

Is It COVID?

Maybe. We can’t say with this analysis. What we’ve done here is effectively drawn a correlation between COVID, which was in effect in 2020 but in no other years, and especially strange results that also occurred in 2020. What we can’t say is that COVID caused the strangeness. Clearly there are variables other than COVID, like whatever went on in 2018, that could also cause strange results. This analysis doesn’t control for any of those variables. We don’t even know what they are. So while at a high level what we’ve seen in our analysis makes sense with what we might expect the impacts of COVID/COVID restrictions on a swim meet or season to be (times get slower versus previous years) we CANNOT say for sure that COVID/COVID restrictions are the cause. We can’t say anything is the cause, this just isn’t that kind of experiment.

We do know, based on reporting from the Democrat and Chronicle, that COVID caused limited off-season workouts, limited access to pools, changes to rest in the meet itself, all sorts of things that as subject matter experts in the sport of swimming we can say would hurt performances.

So is it impacts of COVID/COVID restrictions? From the data, we can’t say. From our swimming expertise though, yeah, it is.

This is how I generally use data - not in a vacuum, but in combination with subject matter expertise. Here the data is probably overkill, no one from the swimming world is likely surprised that this season was slower than previous ones. The point of this exercise isn’t to prove a surprising point, it’s to demonstrate how to do the exercise.

---

In Closing

Once again, thanks for tuning in to another case study here at Swimming + Data Science. We hope to see you next time, when we’ll be doing something else.