Boys Scores

Scores[[1]] %>%
  arrange(desc(Score)) %>%
  mutate(Place = rank(desc(Score), ties.method = "min")) %>%
  select(Place, State, Score) %>%
  flextable_style()

Girls Scores

Scores[[2]] %>%
  arrange(desc(Score)) %>%
  mutate(Place = rank(desc(Score), ties.method = "min")) %>%
  select(Place, State, Score) %>%
  flextable_style()

Overall Scores

Combined_Scores <- Scores %>%
  bind_rows %>%
  group_by(State) %>%
  summarise(Score = sum(Score, na.rm = TRUE)) %>%
  arrange(desc(Score)) %>%
  mutate(Place = rank(desc(Score), ties.method = "min")) %>% # using rank here is important because we actually do have a tie
  select(Place, State, Score)

Combined_Scores %>% 
  flextable_style()

California wins again, but the real story here is Ohio. Ohio was seeded 7th, but finished 2nd today. The heroes for Ohio were the boys from Cincinnati St Xavier, who won all three relays and scored 120 points in doing so.

Results_Final %>%
  filter(is.na(Name) == TRUE,
         Team == "Cincinnati St Xavier") %>%
  select(Place, Team, Finals_Time, Event, Points) %>%
  flextable_style()

Original Assumption

Way back in July, when the State-Off started I made the decision to seed states based on their population. The assumption, which seemed reasonable at the time, was that states with larger populations would have a larger population pool (heh heh) from which to draw potential swimmers, and thus would have more, faster, swimmers than less populous states. Seeding by population made sense, with more populous states expected to defeat less populous ones.

Pop_Data <- read.csv("http://www2.census.gov/programs-surveys/popest/datasets/2010-2019/national/totals/nst-est2019-alldata.csv?#") # download data
Seeds <- Pop_Data %>%
  mutate(STATE = as.numeric(STATE)) %>%
  filter(STATE >= 1) %>%
  select(NAME, POPESTIMATE2019) %>% # get populations
  arrange(desc(POPESTIMATE2019)) %>%
  top_n(8) %>% # cut down to top 8 most populated states
  mutate(Seed = 1:n(),
         POPESTIMATE2019 = round(POPESTIMATE2019 / 1000000, 2)) %>%
  select(Seed, "State" = NAME, "Population_mil" = POPESTIMATE2019) %>% 
  mutate(State = state.abb[match(State,state.name)]) # convert names (California) to abbreviations (CA)

Seeds %>% 
  flextable_style()

Actual Results

In the head-to-head matchups that followed my original assumption was largely born out. There was only one upset, when 5th seeded Pennsylvania upset 4th seeded New York. Otherwise more populous states did defeat less populous ones. Today’s results however don’t show the same trend between population and score, or seed and place.

Score_Pop <- Combined_Scores %>% 
  left_join(Seeds, by = "State")

Score_Pop %>%
  ggplot(aes(x = Population_mil, y = Score)) +
  geom_point(aes(color = State)) +
  geom_smooth(method = "lm") + # add linear fit line, with standard error
  theme_bw()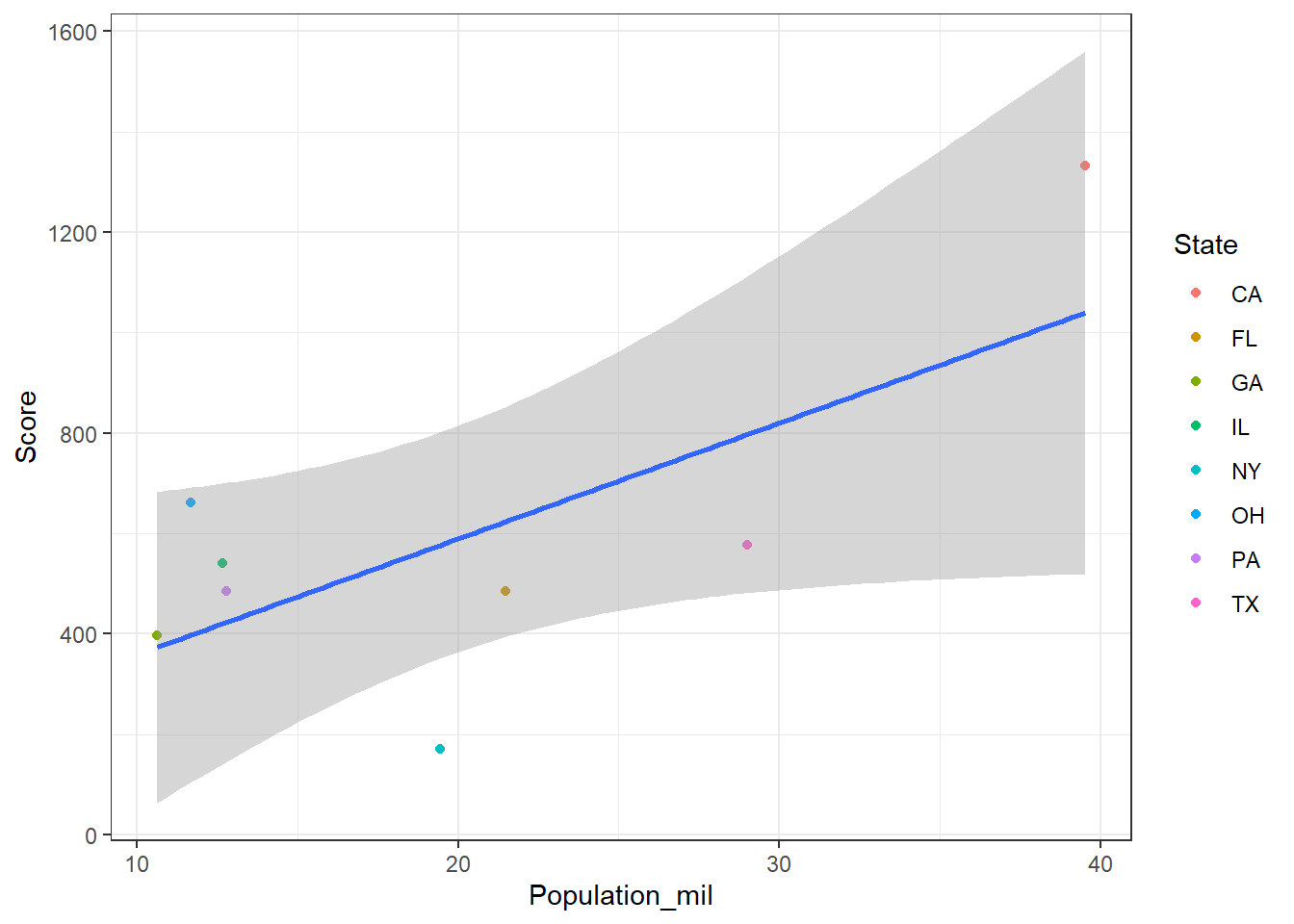

Score_Pop %>% 
  ggplot(aes(x = Seed, y = Place)) +
  geom_point(aes(color = State)) +
  geom_smooth(method = "lm") + # add linear fit line, with standard error
  theme_bw()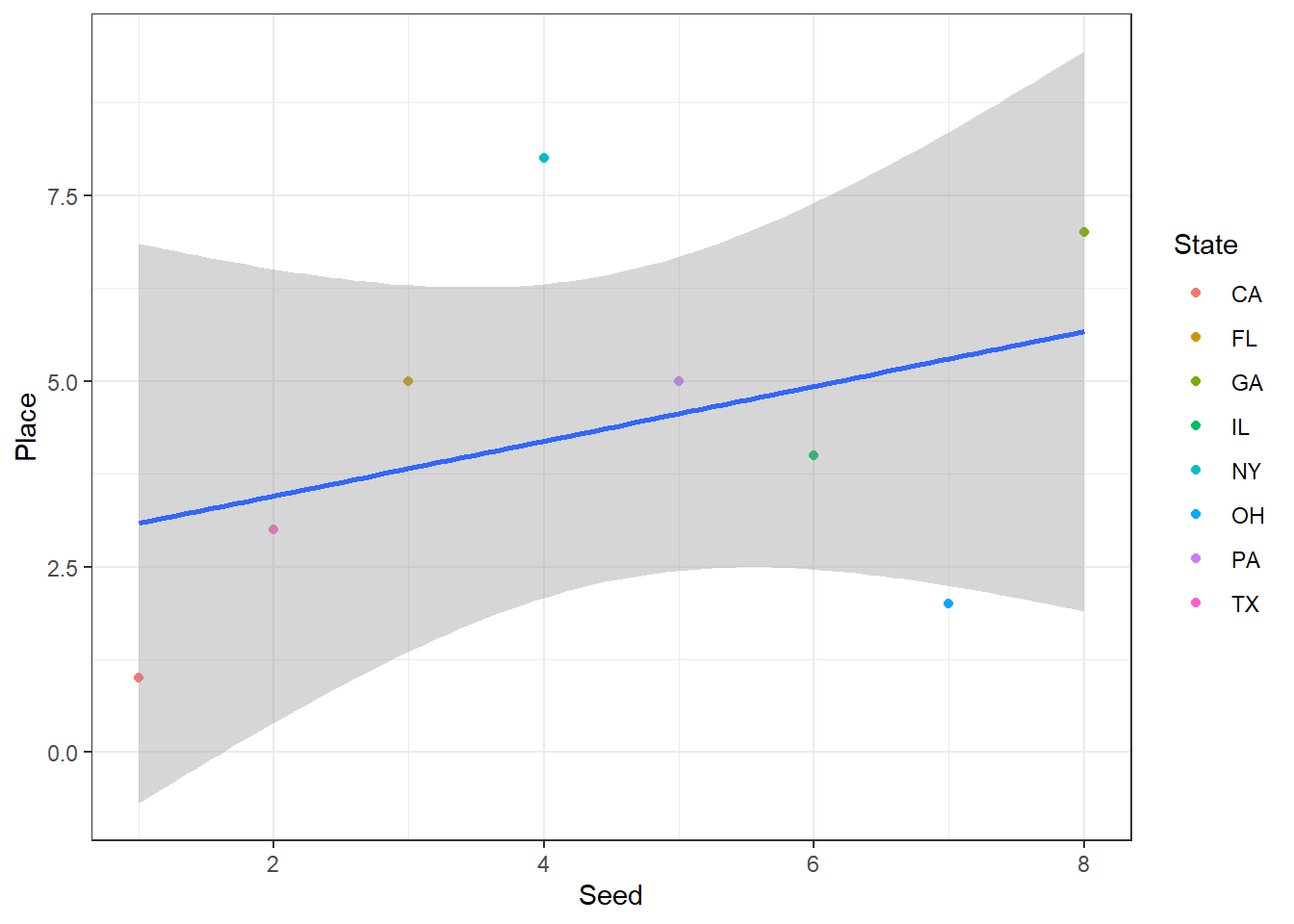

There doesn’t look to be any particular relationship between either population and score, or seed and actual order of finish (place). Population vs. score looks more linear, but I suspect that’s just because California is so far in the upper right corner that it’s just dragging the fit out. We can, should, and in fact will, do some testing to confirm though. One possible relationship between to variables is a linear relationship. There are of course other relationships, but let’s focus on linearity for a moment.

To be clear, my original assumption when I devised the seeding wasn’t that population and score would be linearly related - it was more general. I assumed that score would increase as population increased. The increase could be linear, but could also be exponential, cubic, etc., any of which would have justified population as a seeding mechanism. Built into that original assumption though was a second assumption, which is linear. I assigned seeds based on population, and then earlier in this post we assigned places based on score. Seed and place are in effect ordinal values corresponding to the numeric values of population and score respectively, and if score does increase with population than seed and place should have a linear relationship. We can see such a relationship below. The fit line from geom_smooth intersects each point perfectly. Standard error is also enabled, as in the plots above, but doesn’t show up, because there is no error. The linear fit is literally perfect.

df <- data.frame(Seed = seq(1, 8, 1),
                 Place = seq(1, 8, 1))

df %>% 
  ggplot(aes(x = Seed, y = Place)) +
  geom_point(size = 2) +
  geom_smooth(method = "lm") +
  theme_bw()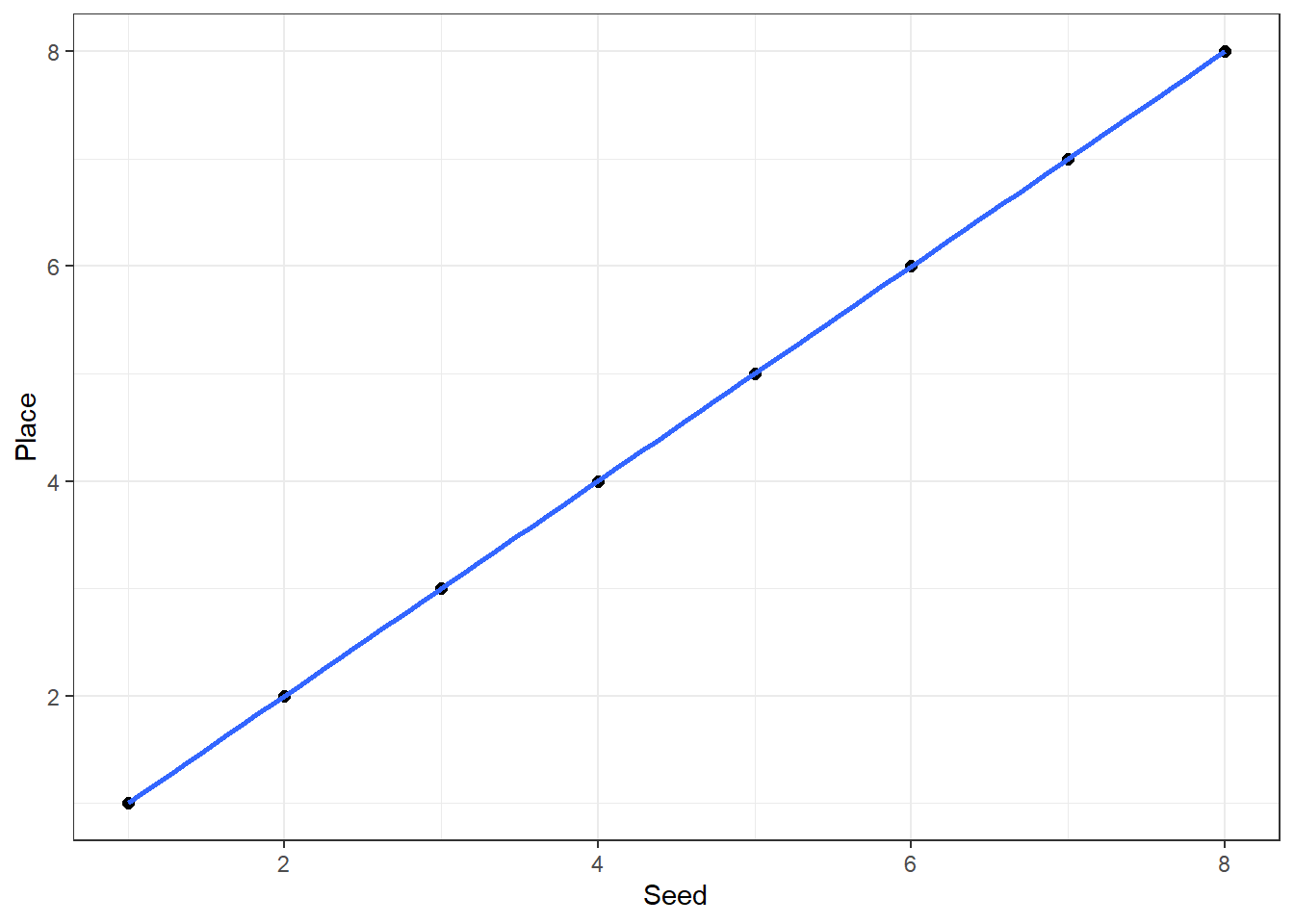

Correlation Testing

I bring all this up because R has the built in function cor.test, which we can use to test for linear correlation. In addition to arguments specifying each of the two variables under test, cor.test also has an argument called method, used to specify the exact statistical test used. The two tests we’ll consider here are Pearson’s (method = "pearson", the default) and Spearman’s (method = "spearman"). Pearson’s test assumes that 1. There is a linear relationship between the two variables. Again, this is the case for seed/place, but need not be for population/score 2. The variables are normally distributed. Let’s test for this.

shapiro.test(Score_Pop$Score)

## 
##  Shapiro-Wilk normality test
## 
## data:  Score_Pop$Score
## W = 0.81856, p-value = 0.04507

shapiro.test(Score_Pop$Population_mil)

## 
##  Shapiro-Wilk normality test
## 
## data:  Score_Pop$Population_mil
## W = 0.85247, p-value = 0.1009

The null assumption for shapiro.test is that the variable is normally distributed. We see that for Score_Pop$Score and Score_Pop$Population_mil the p-values are 0.045 and 0.101 respectively. The value for Score is less than 0.05, so we can reject the null hypothesis and conclude Score is not normally distributed. Between that and the need-not-be-linear relationship between population and score Pearson’s test is out.

That leaves Spearman’s. Spearman’s test does not require variables to be normally distributed, and it doesn’t require a the assumption of a linear relationship between variables. This is because Spearman’s uses a rank method, ordering each variable, assigning a rank, and checking for correlation between those ranks. This sounds a lot like what we’ve already done, ranking population and assigning seed, and ranking score and assigning place. The null hypothesis for Spearman’s test is that there is not a linear relationship between the two variables.

Spearman_Place_Seed <- cor.test(Score_Pop$Place, Score_Pop$Seed, method = "spearman")
Spearman_Place_Seed

## 
##  Spearman's rank correlation rho
## 
## data:  Score_Pop$Place and Score_Pop$Seed
## S = 53.82, p-value = 0.3821
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.3592879

Spearman_Score_Pop <- cor.test(Score_Pop$Score, Score_Pop$Population_mil, method = "spearman")
Spearman_Score_Pop

## 
##  Spearman's rank correlation rho
## 
## data:  Score_Pop$Score and Score_Pop$Population_mil
## S = 53.82, p-value = 0.3821
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.3592879

For both tests our p-value is 0.382, greater than 0.05. We cannot reject the null hypothesis, and so we conclude there is not a linear relationship between seed and place, or between population and score, in today’s meet. Not only are our p-values the same for each test, Our Spearman’s test results are in fact exactly the same, which we can confirm. First, let’s look at the structure:

str(Spearman_Place_Seed)

## List of 8
##  $ statistic  : Named num 53.8
##   ..- attr(*, "names")= chr "S"
##  $ parameter  : NULL
##  $ p.value    : num 0.382
##  $ estimate   : Named num 0.359
##   ..- attr(*, "names")= chr "rho"
##  $ null.value : Named num 0
##   ..- attr(*, "names")= chr "rho"
##  $ alternative: chr "two.sided"
##  $ method     : chr "Spearman's rank correlation rho"
##  $ data.name  : chr "Score_Pop$Place and Score_Pop$Seed"
##  - attr(*, "class")= chr "htest"

Each result has 8 elements, the last of which are the variable names. These will of course be different between tests, because we’re testing different variables. Everything else though is either a result of the test, or an input to the test. We can thus compare everything except the 8th element and expect them to be identical.

identical(Spearman_Place_Seed[1:7], Spearman_Score_Pop[1:7])

## [1] TRUE

The test results are identical because the Spearman’s test does to population and score what we already did in assigning seed and place. As for the test results, correlations are of course not the same as causations. Even if population and score had been correlated for today’s meet we wouldn’t be able to prove that higher population actually causes faster swims and higher scores. For today’s meet population proves to not have a linear relationship with score, nor does another relationship readily present itself.

Boys

Swimmer_Of_Meet[[1]] %>%
  slice_head(n = 5) %>%
  select(-Gender) %>%
  ungroup() %>%
  flextable_style()

Jake Magahey is a fresh face in the Swimmer of the Meet arena. He didn’t win any Swimmer of the Meet crowns during the State-Off Rounds. He wasn’t ever even runner up. Here he is though, top of the heap, in the State-Off Battle Royale. Maybe we didn’t predict it, but that’s why they play the games. On the other hand he was tied for first in the CollegeSwimming 2020 cycle rankings so maybe we could have predicted it after all. Congratulations to Jake!

Results_Final %>%
  filter(Name == "Magahey, Jake") %>%
  select(Place, Name, Team, Finals_Time, Event) %>%
  arrange(desc(Event)) %>%
  ungroup() %>%
  flextable_style()

Girls

Swimmer_Of_Meet[[2]] %>%
  slice_head(n = 5) %>%
  select(-Gender) %>%
  ungroup() %>%
  flextable() %>%
  bold(part = "header") %>%
  bg(bg = "#D3D3D3", part = "header") %>%
  autofit()

Meet the new boss, same as the old boss. Zoie Hartman is well known around these parts, as she swept all the Swimmer of the Meet crowns in the standard tournament. Today is no different, in fact it’s a replay of the California vs. Texas championship meet where Zoie edged out Lillie Nordmann. Congratulations again to Zoie for an extremely successful State-Off run!

Results_Final %>%
  filter(Name == "Hartman, Zoie") %>%
  select(Place, Name, Team, Finals_Time, Event) %>%
  arrange(desc(Event)) %>%
  ungroup() %>%
  flextable_style()